Liquid solvent direct air capture’s cost and carbon dioxide removal vary with ambient environmental conditions

To avert the worst consequences of climate change, we need to achieve more than the deep decarbonization of the energy system. An increasing number of emissions trajectories derived from integrated assessment models of the global climate and energy system also require substantial amounts of carbon removal to stabilize the climate at targets enshrined in the Paris Agreement¹. Overshoot pathways acknowledge that mobilization towards a low-carbon system has been slow and might continue to be so, hence they envision varying numbers of years later in the century during which human activity generates net-negative emissions—in other words, when more carbon dioxide (CO₂) is removed than emitted². Carbon dioxide removal might also be required to offset emissions from energy services that could struggle to transition to low-carbon alternatives, or non-energy-based emissions (such as methane produced by livestock, or CO₂ from cement production)—so-called hard-to-abate subsectors.

This potential need for large amounts of carbon dioxide removal has stimulated research into negative emissions technologies. Among this varied suite of natural and engineered systems is the direct air capture of CO₂ (DAC). Existing literature has noted that DAC comes with high energy and capital requirements; our work is designed to provide a more informed weighting of DAC’s deployment potential relative to other mitigation options.

Typically, DAC is accomplished through the absorption or adsorption of CO₂ into solvents or onto sorbents, respectively. Several DAC pilot or small-scale plants exist, and it is now approaching the commercial demonstration level of technology readiness for larger-scale plants, on the order of 10² to 10³ ktCO₂/year. Despite the technology’s relative novelty, the large carbon management infrastructure it requires³, and previous warnings about prematurely relying on it⁴, policymakers are increasingly expecting negative emissions technologies to contribute to decarbonization. For example, in its long-term strategy submission to the United Nations Framework Convention on Climate Change, Canada’s modelled approaches for achieving its legislated net-zero emission target could involve large amounts of DAC deployment, with upper bounds of 200 Megatonnes of CO₂ (MtCO₂) removal through DAC by 2050⁵, depending on scenario. For context, Canada had 3 MtCO₂ of operational capture capacity at the end of 2022⁶; globally, 49 MtCO₂ was captured in 2023, all from point sources of carbon emissions⁷.

Two leading DAC technologies are the solid-sorbent-based capture technology developed by Climeworks⁸, and the liquid-solvent-based capture technology developed by Carbon Engineering⁹. For example, the deployment of these technologies at the Megatonne scale, through the US Regional Direct Air Capture Hubs programme, will represent capture rates two orders of magnitude greater than any existing DAC facility¹⁰. In our model, we consider the latter technology, comprising a potassium hydroxide-based absorption system with a potassium loop and a calcium loop. In the potassium loop, atmospheric CO₂ dissolves into the solvent, forming a carbonate. In the calcium loop, the carbonate ion is removed, regenerating the potassium hydroxide, and the CO₂ is liberated and prepared for transmission and storage. The technology has been modelled and demonstrated^9,11, and results of those models integrated into broader systems-level studies that consider DAC’s emergency deployment potential³, life cycle impacts¹², and power system impacts¹³. However, little research considers how this technology’s operation in the real world would be greatly affected by climate. Ambient air temperature, pressure, humidity, and CO₂ concentration all vary—some enormously and within short spans of time—and these variations will greatly affect capture rates and could occasion plant shutdown. This work complements similar analyses for solid-sorbent DAC by Cai¹⁴, Sendi¹⁵, and Terlouw¹⁶. For liquid-solvent DAC, An¹⁷ developed a model that is limited to a subset of temperature and humidity ranges, does not consider ambient pressure or CO₂ concentrations, and cannot be replicated without proprietary software.

Here, we make several contributions to the literature on DAC’s potential role in the deep decarbonization of energy systems. One: we model the performance of a DAC plant in the real world, where ambient conditions greatly affect capture. Two: we extend this analysis across all of Canada, a jurisdiction that has expressed interest in deploying DAC at some of the largest scales. We develop estimates of the cost and performance penalties that climate conditions incur on DAC plants. Three: we develop an open-source chemical process model of liquid-solvent DAC (Methods). Unlike models built using expensive or proprietary programmes, ours can be employed or adapted to support investors, analysts, and policy makers.

Process response to inlet conditions

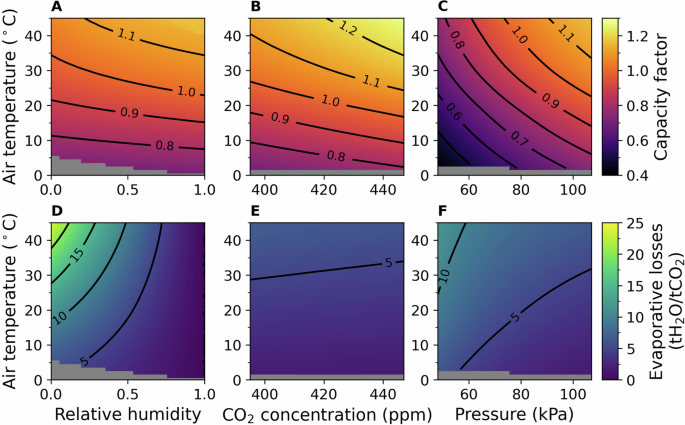
The performance of a nominal 1 MtCO₂ gross capture facility (see supplementary information (SI) note S3 for plant specifications) was simulated for a range of possible ambient environmental conditions, modelled as inlet conditions at the capture unit (contactor). At nominal conditions, the model predicts the CO₂ captured at 97% of the published predicted annual total (details in the SI, note S4)⁹. Conditions considered were ambient air temperature, pressure, humidity, CO₂ concentration, and liquid solvent temperature. The range of conditions simulated is tabulated in the SI (Table S7). We consider evaporative losses, as the large volumes of air processed through the contactor (approximately 57,000 m³ s⁻¹) are free to absorb moisture from the aqueous solvent. As the contactor is designed to maximize surface area for the absorption of CO₂, so too does it act as a very efficient evaporator. Makeup water is required to replace these evaporative losses. Performance of the plant in terms of capacity factor (CF) (1) and evaporative losses (2) is summarized in Fig. 1. The power required per tCO₂ captured is largely insensitive to environmental conditions, with the exception of fan work at the contactor, where lower air densities require higher volume flow rates to achieve the specified mass flow rate. Performance in terms of the energy intensity of capture are summarized in SI Fig. 8. The liquid inlet temperature is assumed to be at equilibrium with the ambient air temperature. Inlet (solvent and air) temperatures at or below 0 °C are not simulated, as we model the thermodynamic properties of the solvent as pure water, and these temperatures represent freezing conditions (KOH and K₂CO₃ in solution are expected to depress the solvent freezing temperature by approximately 3 °C). Engineering solutions can enable operation in sub-zero temperatures—these include active heating of the inlet air. However, this would be a large additional process load due to the dilute concentrations of CO₂. For example, air at 0.06% CO₂ by mass, assuming a 100% capture rate, requires the heating of 99.94 t-air per tCO₂. If we assume a heat capacity of 1 kJ kg⁻¹ K⁻¹, this represents a heating load of approximately 0.03 MWh tCO2−1 per K heated.

Over the range of conditions simulated, we see the greatest change in capture rates over the ambient temperature range, followed by pressure, CO₂ concentrations, and lastly humidity. Higher ambient temperatures increase reaction kinetics, modelled via correlations for the reaction rate constant, ion diffusivity, liquid-phase mass-transfer coefficient, and the CO₂ reference solubility for use in Henry’s Law. Higher pressures and CO₂ concentrations both increase the CO₂ partial pressure, which proportionally increases the interface concentration (9), directly increasing the capture rate (7). We see the least change in capture rates over the humidity range, as humidity only indirectly affects capture rate by lowering or raising the liquid temperature via evaporation and condensation, respectively. Evaporation rates are modelled as driven by the difference of the humidity ratio and saturated humidity ratio at the liquid temperature (see Methods), and as such are driven strongly by both humidity and temperature. As warm air can absorb much more moisture than cold air, the highest evaporation rates are when the air is both dry and warm. Pressure has a milder influence on evaporation, with increasing pressure decreasing the saturated vapour pressure (SI equation S12). CO₂ concentrations have no direct effect on evaporation, only lowering the evaporative losses when normalized by the CO₂ capture rate.

Regional variations affect overall plant performance

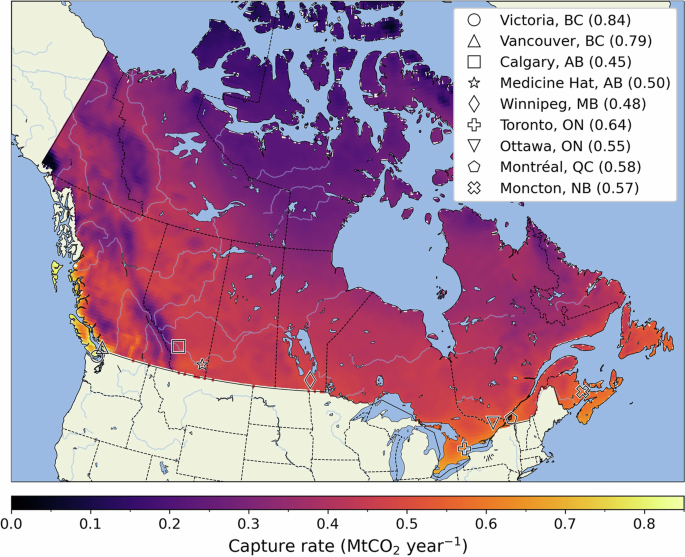
We use hourly climate data to predict changes in performance for the same 1 MtCO₂ plant as a function of differentiated and variable climate conditions. Regional environmental profiles influence capture rates, evaporative losses, and the intermittency of plant operation. Contactor operation requires air temperatures above freezing, leading to strong seasonal intermittency in operation within the temperate latitudes examined. Regional differences in capture rates across Canada are shown in Fig. 2, with energy use and evaporative losses shown in the SI (Figs. S3 and S4, respectively). With respect to CO₂ capture, we see the expected decrease in capture with latitude, as average temperatures decrease, although regional geographic features can dominate a microclimate. For example, on the west coast, the ocean has a strong regional effect in moderating winter temperatures, and here we find the highest annual capacity factors (over 0.8) in the country (this effect is less pronounced on the east coast, due to the colder Labrador current). However, adjacent to the Pacific coast, we find some of the least-suitable climes for DAC (CF near 0.2), among the low temperatures and high altitudes of the Coast Mountains and Rocky Mountains.

Evaporative losses are highest over the Prairies, which is important as this region also represents the highest solar resource potential in Canada. However, it is also Canada’s breadbasket, and competition for water resources by DAC is an additional cost of deployment. Solar resources, which could provide a low-cost, low-emission power source for DAC, are often correlated with existing water-stress. Of the locations identified in Fig. 2, the lowest annual evaporative losses occur in Toronto, Ontario (ON) (1.84 tH₂O tCO2−1), and the highest in Medicine Hat, Alberta (AB) (4.51 tH₂O tCO2−1). The energy intensity of capture has little regional variation, with Fig. 2 locations representing a range of 1.80 to 1.87 MWh tCO2−1. The highest energy use within the study region (2.06 MWh tCO2−1) occurs over extreme elevation, where low pressures increase contactor fan and CO₂ compression loads.

Plant operation will be dynamic, potentially intermittent

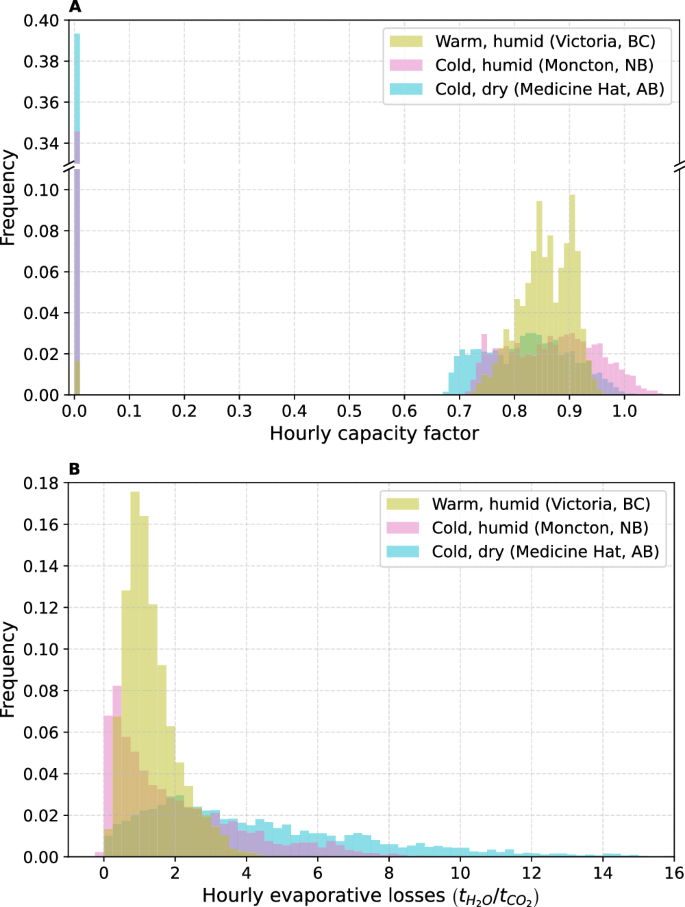
Varying ambient conditions will necessitate dynamic DAC plant operation and control. We analyze plant performance in locations that are representative of the most prevalent climate regions studied, outside of polar and sub-arctic climes that include the Northern Territories. These archetypal locations include Victoria, British Columbia (BC), Medicine Hat, AB, and Moncton, New Brunswick (NB), representative of warm-humid, cold-dry, and cold-humid climes, respectively. Figure 3 shows the annual distribution of hourly capacity factors and evaporative losses that would be expected from DAC plants deployed at each of the three locations. Annual performance summaries, as well as climate classification of the regions within the Koppen climate classification scheme, are given in the SI (Table S8).

The capacity factors shown in Figs. 2 and 3 are an upper bound: they represent the sum of the hourly capture as a function of varying environmental conditions, relative to 1 MtCO₂ of annual capture. In other words, they ignore the feasibility of starting up and shutting down a large and complex chemical plant on hourly timescales, when plant startup in process industries could take hours to weeks. In the temperate latitudes considered, there are typically times of the year when air temperatures fluctuate around 0 °C, so that air temperatures are only intermittently suitable for plant operations.

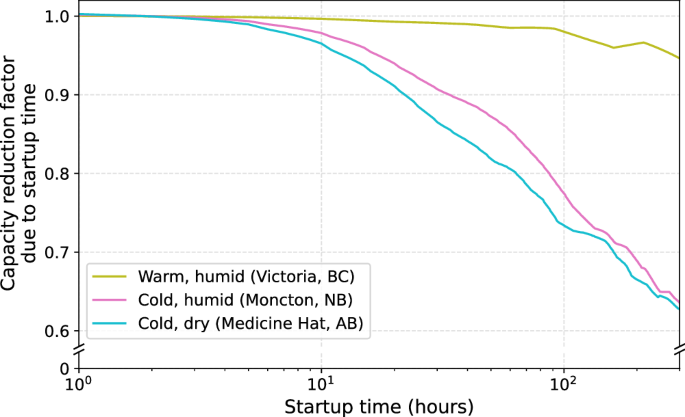
In Fig. 4, the effect of intermittency on performance is explored by incorporating a plant startup time: the time it would take to restart the plant after shutting it down to prevent the solvent from freezing. A startup time of 1 hour represents our maximum capacity factor, since we use hourly climate data in calculating earlier capacity factors. The ordinate, the capacity reduction factor, is the ratio of the capture capacity—reduced by startup time—to the maximum capture capacity. The capacity reduction factors in Fig. 4 further emphasize the importance of ambient conditions to liquid-solvent DAC plant siting. For example, a startup time of 100 hours—or roughly four days—could de-rate plant performance by 5–25%. Calciner startup, including preheating, may provide a minimum startup time of approximately 10 hours^18,19. However, these plants comprise many tightly coupled units, including heat exchangers. Start-up times could therefore exceed this.

The feasibility of avoiding shutdown by pre-heating the air was estimated above at 0.03 MWh tCO2−1 K⁻¹. Heating the solvent represents a lower energy demand, with approximately four times the heat capacity of air, but one-eighth of the mass flow rate. However, strong evaporative cooling would require heating of the solvent well beyond the freezing point. For example, at nominal humidity and pressure, inlet air at –1 °C would require heating of the solvent to 7 °C to avoid freezing. While these represent large loads for active heating, this could be an opportunity for passive solar or low-quality geothermal heat.

Levelized cost of CO₂ captured from the atmosphere

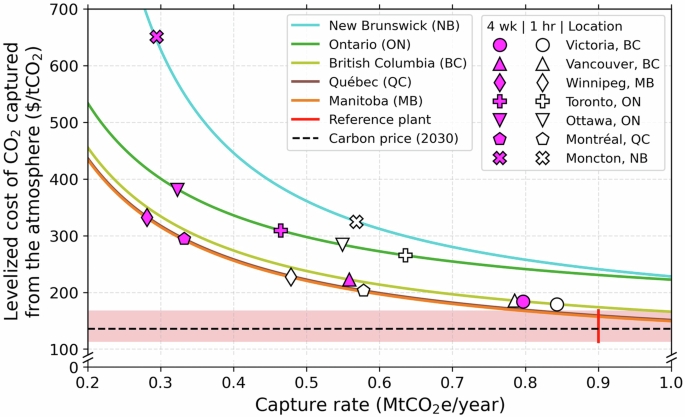
A levelized cost of CO₂ captured from the atmosphere (LCOR) is estimated based on plant capital costs (CapEx) of 1 billion US dollars (USD)⁹, provincial electricity prices for large industrial consumers²⁰, average provincial electric grid carbon intensities²¹, capacity factors, and location-specific energy intensities of capture (see SI Tables S8–S9). The LCOR does not include costs or emissions associated with the transportation or storage of the captured CO₂ but does include the energy required for compression to typical pipeline pressures. Embodied emissions from the construction of the plant have not been included but are estimated elsewhere at 0.00088 tCO₂ tCO₂-captured^−1 22. A discount rate of 5 per cent and a capital amortization period of 25 years allow for comparisons of cost estimates with⁹. The procedure for calculating LCOR are given in the methods ((32)–(36)). The LCOR for a plant with a 1-hour versus 4-week startup time is calculated. The resulting LCOR are shown in Fig. 5. All prices are given in USD.

We assume that the DAC plant is wholly electrified. We have made the simplifying assumption that the capital cost of an electrified plant is equivalent to the reference process, at 1B USD. In modelling the operational expenses, we restrict ourselves to the energy requirements of the five main process steps (see Methods): absorption, precipitation, calcination, slaking, and compression (other operational or maintenance costs are ignored). Regarding the reference process and since the plant is assumed to be electrified, we do not model the power island, CO₂ absorber (on turbine exhaust), oxygen plant (air supply unit), or the combined auxiliary loads comprising 2.6 MW. As discussed elsewhere²², indirectly heated calciners suitable for electric resistance heating are commercially available, but not at the scale considered here, and would require a dedicated fluidizing gas. At the nominal operating conditions, the capture energy is predicted to be 1.80 MWh tCO2−1. At this capture energy, an electric grid carbon intensity of 555 gCO2kWh−1 yields no net capture of CO₂. Therefore, it would be counterproductive to use grid electricity for DAC in Nova Scotia, Saskatchewan, or Alberta, since electric grid carbon intensities in those provinces exceed this threshold due to their overwhelming reliance on fossil fuels—something that is peculiar in the Canadian context, where electric power grids are relatively cleaner than they are elsewhere in the world.

We see a range of LCOR values in Canada, with the most favourable regions yielding values of approximately 190 $ tCO2−1. This can be compared to estimates for nominal operating conditions at 90% utilization of 113–168 $ tCO2−1⁹. Inexpensive and low-carbon electricity, such as in Québec, can result in regions with low capacity factors having a competitive LCOR compared to regions with more favourable climate conditions, such as British Columbia. These prices can also be compared to the (Canadian) Federal Government’s projected 2030 price on carbon of 134 $ tCO2−1 (170 CAD tCO2−1)²³. A map of the regional distribution of pricing for Canadian provinces is included in the SI, Fig. S10.

Jurisdictions considering large levels of future carbon removal through direct air capture must decide where these chemical process facilities will be sited. In addition to considerations regarding transportation, storage, and social acceptance, these facilities will contend with a more fundamental technical challenge: their capture rates (and thus their carbon removal costs) are going to depend on ambient environmental conditions like temperature, relative humidity, and pressure, among others. Across most of Canada, seasonal freezing temperatures will result in lower capacity factors for liquid solvent DAC technologies. Where the climate is amenable to such a process, the availability of low-carbon energy must also be considered, as net carbon removal is the measure of success. Combining regional climate profiles, energy emissions intensities, and energy prices, we can offer an initial estimate of region-specific carbon removal costs. For jurisdictions that wish to build liquid solvent DAC plants within their borders, these estimates can be used to calibrate policy and investment decisions. Policy makers can consider our results in calibrating the contribution of DAC to their net-zero emission plans, as well as the size of proposed incentives. In addition, policymakers and investors can use our results to guide early investments in CO₂ transportation and storage infrastructure.

Our results show that, for temperate climes, plant startup times should be kept short. Unlike electric power plants, chemical process plants may need anywhere from hours to days to restart, depending on the design and integration of their units. Designing-in protocols for rapid startup that accommodate intermittent operation would be a prudent step on the part of engineers. Arwa demonstrates a method for decoupling the capture and recovery loops for better integration of liquid-solvent DAC with intermittent renewable generation²⁴. This approach could also have benefits for climate-driven intermittent capture.

Energy system modellers must represent complex chemical processes with greater fidelity in their models, to better understand the opportunities and challenges associated with these processes in the energy transition. Ignoring ambient conditions or intermittent operation could have profound implications on energy system operations, including power system reliability, especially as more chemical processes are electrified or converted to electrofuels that are also dependent on electricity for their synthesis.

Our cost and performance estimates should be considered as lower bounds. Future demands for labour and materials, not to mention the energy required for carbon removal will be global in scale, meaning that DAC plant deployment in any nation will not only compete with deployment in other jurisdictions but also with concurrent mitigation efforts in all sectors of the economy. It should also be considered that there is no full-scale trial data with which to validate these predictions, and the model should be reconsidered as these data become available.

Finally, our results focus on one (albeit more technologically mature) liquid solvent DAC technology. The capture model can be readily adapted to alternative aqueous liquid solvents through the inclusion of the appropriate chemical-specific correlations, specifically the salt-effect parameter, reaction rate constant, and ion diffusivity. Solid sorbent DAC systems will behave differently across ambient conditions; their performance is also dependent on the sorbent used. It may be that liquid-solvent and solid-sorbent DAC develop as complementary technologies, as they favour warm-humid and cold-dry¹⁵ climates, respectively. Methods for the intermittent operation of solid sorbent DAC plants could also differ from those for liquid solvent systems. Investors and policy makers should consider these differences as they make decisions regarding the deployment of a portfolio of carbon removal technologies in pursuit of net-zero emission targets.

Chemical process

We develop an open-source model in the Python programming language of a potassium hydroxide-based liquid-solvent DAC process described elsewhere⁹. There are five main process steps. One: dissolution and binding of atmospheric carbon dioxide (CO₂) within the contactor, in the form of potassium carbonate (K₂CO₃) (3). Two: precipitation of calcium carbonate (CaCO₃) within the pellet reactor (4). Three: liberation of CO₂ within the calciner (5). Four: hydration of quicklime (CaO) to slaked lime (Ca(OH)₂) within the lime slaker (6). Five: compression of the concentrated CO₂ for transport and utilization or storage. Process modelling is limited to the contactor, which, when combined with the inlet flow conditions, determines both the capture rate of the facility and the evaporative losses. Mass and energy balances are performed for the main process steps to generate estimates of the plant’s mechanical and thermal energy loads. Thermal and mechanical loads are treated as equivalent from a load perspective, when estimating the total power requirements. Heat integration is assumed at 50%, with the manner of energy recovery not considered. Energy recovered from heat integration is discounted directly from the power load.

Modelling the contactor

The contactor is modelled as a 1-dimensional counter-flow packed column. Ambient air at mass flow rate m˙G enters at the bottom of the contactor and is forced through the column, while the liquid solvent at mass flow rate m˙L enters at the top. The column is filled with random or structured packing to increase the specific surface area available for mass transfer a, without excessive pressure drop across the column.

CO₂ capture process

Whitman’s film theory²⁵, ²⁶ is used to predict the gas-to-liquid CO₂ mass transfer rate JL,CO2(7), which is the product of the liquid-phase mass transfer coefficient k_L(8), estimated by Onda’s correlation²⁷, the interface concentration ci,CO2(9), determined using Henry’s Law for solutions, and the enhancement factor E ((10)–(12))²⁵. In finding k_L, additional correlations for the effective packing diameter d_p, wetted area a_w, and diffusivity D are used (these are given in SI Table S4). Other terms in the equations below include the kinematic viscosity ν, acceleration due to gravity g, and liquid superficial velocity U_s.

To solve for E requires: (a) the second-order rate constant k₂ for the reaction of CO₂ and KOH, with correlations elaborated by Pinsent²⁸ and Kucka²⁹, and included in SI Table S4; (b) the diffusivity of liquid-phase CO₂ DL,CO2 as correlated by Wilke & Chang²⁵, which can also be found in Table S4; (c) the diffusivity of the binding species (OH⁻) D_B, as correlated by See³⁰ for temperatures 1≤T_L≤25 °C, and the Stokes-Einstein method³¹ for T_L >25 °C; and (d) the stoichiometric coefficient z of the binding species (in this case 2, see equation (3)), where E_i is (12) the enhancement factor for an instantaneous reaction.

The Henry’s Law constant H is a function of liquid temperature and ionic strength (13). The reference solubility of CO₂ in pure water H⁰(T) is predicted using the Van’t Hoff extrapolation³²(14), where the reference temperature T₀ = 298.15 K, H⁰(T₀) = 3.4 × 10⁻² atm L mol⁻¹, the enthalpy of solution Δ_solH = − 19.95 kJ mol⁻¹³³, and R is the molar gas constant. Following the method of van Krevelen and Hoftikzer²⁵, H in solution is correlated to H⁰ by the ionic strength I(15) and Setchenov salt-effect parameter h(16), where c_i is the concentration of ions in solution with charge z_i, and h₊, h₋, and hCO2 are the salt-effect parameters for the positive ions, negative ions, and dissolved CO₂ in solution, respectively.

To predict the total capture rate, the column is discretized into n finite volumes spanning the diameter of the column, of volume dV. Conditions are modelled as steady within each volume. For each volume i, the mass capture rate m˙CO2,i is the product of JL,CO2; the area available for capture A_c(17); and the molar mass of CO₂ MCO2. The packing efficiency, η_pack, accounts for the incomplete wetting of the packing at low solvent flow rates (we use the value provided by Holmes and Keith of 0.80¹¹).

Evaporation and condensation

Evaporation and condensation rates m˙vap(20), with associated heat transfer, are also estimated for each volume, following the method described by Sutherland³⁴, where the evaporation rate is driven by the difference in the air humidity ratio ω and the saturated humidity ratio ω_sat at the liquid temperature. The convective mass-transfer coefficient ϕ is predicted by an empirical correlation from cooling tower data described by Kuehn (21)³⁵, where c and n are coefficients fitted to the specific column under analysis, within the range 1.0≤c≤1.7 and 0.25≤n≤1.0, and V is the total column volume. In the absence of experimental data, the recommended values³⁵ of c = 1.3 and n = 0.6 are used.

Sensible and latent heat transfer occurs between the gas and liquid phases within the column, with the packing and column walls modelled as adiabatic. Energy released from the reaction of CO₂ with KOH is ignored: as the liquid molar flow rate is 2-3 orders of magnitude greater than the reaction rate, the resulting liquid temperature changes are negligible ( ≈ 2 × 10⁻³ K at 20 °C). Thermodynamic properties of the gas and liquid phases are modelled as moist air and water, respectively. Convective heat transfer rates are correlated to evaporation rates using the Lewis number Le (22), sometimes referred to in this form as the Lewis relation, which is the ratio of the convective heat-transfer coefficient ζ to the mass-transfer coefficient ϕ, normalized by the specific heat capacity of moist air c_m. For air and water vapour mixtures near atmospheric pressures Le = 0.9³⁶.

Convective heat transfer based on sensible heat difference is exchanged between the gas and liquid phases (23), while latent heat due to vaporization and condensation is exchanged with the liquid phase (24), where h_vap (J kg⁻¹) is the enthalpy of water vapour at the temperature of the liquid. The temperature change dT ((25), (26)) is found from the change in enthalpies (dh_G, dh_L) and the specific heat capacities (c_m, c_L) of the gas and liquid phases, respectively. Note, h_L is defined as joules per kg of dry air. A diagram of the heat and mass transfer across a single column element is given in the SI (Figure S1).

Solution method

The model comprises a steady-state solution for heat transfer and H₂O and CO₂ mass transfer between the gas- and liquid-phases within the contactor. To arrive at the solution, the column is discretized spatially into a 1-dimensional array of volume elements between the inlet and outlet. Evaporation and heat exchange rates for each element are solved using the forward Euler method, which iterates until convergence. The evaporation solution is used as the input to find the CO₂ absorption rates, which are similarly solved using an iterative backward Euler method. A schematic of the element-wise energy and mass balances are given in SI Fig. S1, and of the overall solution procedure in SI Fig. S2. The code is written in Python and published under an open license via CC BY-NC-SA 4.0.

Power consumption

Estimates of contactor power consumption are based on solvent pumping and fan work. In both cases, the power P is a function of the volumetric flow rate Q, pressure drop Δp, and efficiency η(27). In the case of solvent pumping, the pressure drop Δp_L is modelled as the hydrostatic pressure loss over the height of the contactor H(28). In the case of fan work, a pressure drop Δp_G correlation is provided by the vendor of the packing modelled for this study¹¹, where Z is the depth of the packing and U_s is the superficial gas velocity (29). While generalized pressure drop correlations are available³⁷, they are fitted to higher flow-rate data, and over-estimate the pressure drop for this relatively low flow-rate application. The total solvent pumping efficiency η_pump(31) is the product of the driver efficiency η_d and the intrinsic efficiency η_i(30)²⁵.

Pellet reactor

Transfer of carbon from the potassium loop to the calcium loop through precipitation as CaCO₃ takes place within a recirculating, fluidized-bed pellet reactor. The bed height h_bed, fluidization velocity U_mf, and average pellet diameter d_p are parameters taken from the nominal plant as described elsewhere⁹. Similar to the contactor, the energy required is estimated based on the pump work. The pressure drop Δp_bed is the balance of the drag force with the gravitational force on the particles³⁸. Void fraction modelling is described in the SI (note S1). The total pump efficiency is calculated as for the contactor. The total CaCO₃ fines-to-disposal or makeup rate is assumed to be 1% of the CaCO₃ produced⁹.

Calciner

Energy for calcination is modelled as the sum of the thermodynamic energy of the calcination reaction, 178.3 kJ mol⁻¹⁹, and the energy required to raise the sensible heat of the CaCO₃ input stream to the reaction temperature of 900 °C, having a specific heat of 834.3 J kg⁻¹ K⁻¹. Thermal and conversion efficiencies of 78% and 98%, respectively, are taken from ref. ⁹.

Lime slaker

Quicklime from the calciner is hydrated to slaked lime within the lime slaker. Mechanical energy consumption is estimated at 17 kWh per tonne of quicklime³⁹. Conversion efficiency is assumed at 85%⁹, producing thermal energy at 63.9 kJ mol-converted⁻¹. Additional thermal energy is available from reducing the sensible heat of the input CaO stream from 900 to 300 °C. We assume that the thermal energy produced is integrated into plant operations by a heat integration factor η_hi = 0.5.

CO₂ compression

The concentrated CO₂ stream is cooled and compressed for transport and subsequent utilization or storage. Thermal energy is released through reducing the sensible heat of the CO₂ stream from 900 to 40 °C. Similar to the lime slaker, we assume that this energy is integrated at η_hi = 0.5. To estimate the mechanical power required, compression is modelled as isothermal (see SI note S2). In this study, the outlet temperature and pressures are assumed 40 °C and 15.1 MPa, respectively.

Inlet air physical properties

These, comprising temperature, pressure, humidity, and CO₂ concentration, are determined by ambient environmental conditions at the plant site. We consider hourly environmental conditions throughout Canada in 2019. Hourly surface air temperature, relative humidity, and pressure data are taken from the fifth major global reanalysis produced by the European Centre for Medium-Range Weather Forecasts⁴⁰. CO₂ levels (available at three-hour intervals) are taken from the Copernicus Atmosphere Monitoring Service global greenhouse gas reanalysis⁴¹. We conduct the analysis for Canada; grid cells entirely over water are not considered. For each cell, performance is predicted hourly over the sample year of 2019. Spatial and temporal modelling resolutions correspond to the resolutions of the European Centre for Medium-Range Weather Forecasts’ dataset.

Levelized cost of CO₂ captured from the atmosphere

A levelized cost of CO₂ captured from the atmosphere (LCOR) (36) is estimated based on plant capital costs (CapEx) of 1B USD⁹, regional electricity prices for industrial consumers²⁰ (EP), average provincial grid emission (GE) carbon intensities (CI)²¹, annual capacity factor (CF), and location-specific energy intensity of capture (all prices are given in US dollars (USD)). A discount rate r = 0.05 and a capital amortization period of n = 25 years give a capital recovery factor (CRF) of 0.071 (32), which allows comparisons of cost estimates with Keith at CRF = 0.075⁹. Regional pricing, grid emission intensity, and the resulting LCOR are summarized in SI Table S9 and presented in Fig. 5.